Regression Evaluation Metric

안녕하세요. 요즘 블로그 포스팅에 좀 소홀하게 된 것 같은데 이제부터는 1주일에 최소 1개의 포스팅을 아마 하게될 것 같습니다!!

 

현재 Dacon의 제주 신용카드 빅데이터 대회에 참여하고 있는데 오랜만에 경험하는 회귀 예측 문제여서 다시 초심으로 돌아간 마음으로 대회에 임하고 있습니다.

 

머신러닝에서 회귀 예측은 분류문제와 다르게 1 or 0 / True or False / 남자 or 여자 등의 카테고리컬한 변수를 예측하는 것이 아닌 예측하기 위한 설명변수들이 있고 그 설명변수가 예측하는 타겟 변수가 연속적인 값의 형태를 띄며 그것을 예측하는 것을 말합니다.

 

가령, 키, 몸무게, 매출, 수요 등의 예측 문제 이에 속합니다.

 

그래서 연속형 변수들을 예측할 때는 분류 문제처럼 완전 정확하게 예측하기란 불가능에 가깝기 때문에 분류문제에서의 평가 척도와 다른 척도들을 이용합니다.

 

분류문제에서는 Confusion Matrix로 추출할 수 있는 값들(민감도, 재현도, 정확도 등)이 평가 지표로 많이 사용되지만, 회귀문제에서는 예측값과 실제값의 오차를 얼만큼 되는지를 평가 척도로 사용하기 때문에 RMSE, RMSLE, MSE 등이 많이 사용됩니다.

 

이번 포스팅에서는 이러한 회귀 문제에서 사용되는 평가 지표들이 어떤 것들이 있으며, 해당 지표를 구하기 위한 수식과 예측할 때 어떤 척도가 더 많이 사용되며, 그 이유에 대해서 설명드리고자 합니다.

 

1. Regression Metric

- MSE(Mean Squared Error)

평균 오차 제곱합이라고 불리며 실제값과 오차의 차를 제곱한 뒤 평균을 한 값으로 산출합니다.

 

- RMSE(Root Mean Squared Error)

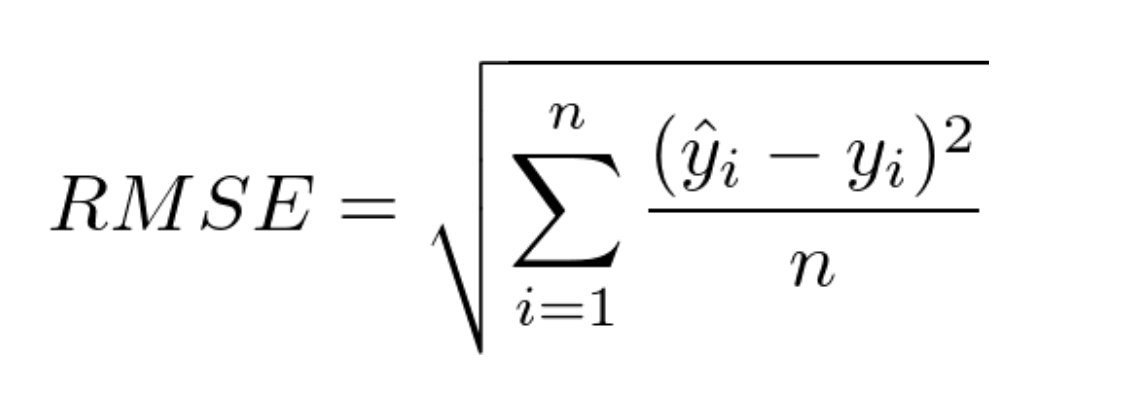
RMSE는 평균 오차 제곱합(MSE)에 루트를 씌운 값으로 단순 오차 제곱합의 오차율 값이 큰 것을 보정해주며, 대표적인 회귀 척도로 많이 사용됩니다.

 

- RMSLE(Root Mean Squared Log Error)

RMSLE는 RMSE의 각 인자에 로그화를 취해준 값으로 연속적인 값의 분포가 치우쳐져 있거나 정규 분포를 따르지 않고 불균형한 모형일 때 사용되는 방법으로 기존의 RMSE보다 값의 비대칭성에 강한 것을 알 수 있습니다. 또한 y=0 일 때 log y 가 Infinity로 수렴할 수 있어서 자유도 1을 더해서 그 케이스를 보정합니다.

 

- MAE(Mean Absolute Error)

MAE는 실제값과 예측값의 차이의 절대값 합의 평균입니다.

 

- MSLE(Mean Squared Log Error)

RMSLE값과 마찬가지로 MSE값에 로그를 취해줘서 산출합니다. MSLE도 마찬가지로 자유도(1)를 더해줘서 무한대가 나오는 경우를 막습니다.

 

- R2(R-Squared)

R2는 총제곱합(SST)에 대한 회귀제곱합(SSR)을 뜻하며 결정계수라고도 불립니다.

결정계수는 반응변수의 변동량(분산)에서 현재 적용(만든)모델이 설명할 수 있는 부분의 비율을 뜻하므로 1에 가까울 수록 설명력이 높다고 말합니다.

 

이외에 MGD(Mean Gamma Deviance), MPD(Mean Poisson Deviance)의 평가 척도도 존재하지만 주로 사용하지 않는 지표이므로 이번 포스팅에서는 넘어가도록 하겠습니다.

 

 

2. RMSE vs RMSLE

위에서 다양한 Regression의 평가 척도로 사용되는 다양한 지표들을 확인해봤는데요.

 

R2는 1에 가까울수록 좋은 성능을 나타내지만, 나머지 MSE, RMSE, RMSLE 등의 지표는 0에 가까울수록 즉, 오차가 적을수록 좋은 성능을 나타낸다고 할 수 있습니다.

 

따라서 회귀 모델의 평가 지표로 사용하실 때는 해당 데이터 및 방법론에서의 적절한 Metric를 결정하여 사용하셔야 합니다.

 

지금부터는 제가 사용하게될 모델 평가 척도인 RMSLE에 대해서 알아보고자 합니다.

RMSLE는 RMSE에 로그를 취해준 것인데요. 로그를 취해준 방법이 기존의 RMSE랑 어떻게 다르고 RMSE에 비해서 어떤 강점을 갖는지 알아보고자 합니다.

 

일단 크게 세가지로 나눌 수 있습니다.

 

1. Outlier Robust

2. 과소평가된 항목에 큰 패널티를 부여한다

3. 상대적 ERROR 측정

 

 

먼저, 1. Outlier Robust에 관한 내용입니다.

 

RMSLE는 이상치에 견고한 성격을 보입니다. 아래의 예시를 함께 보시겠습니다.

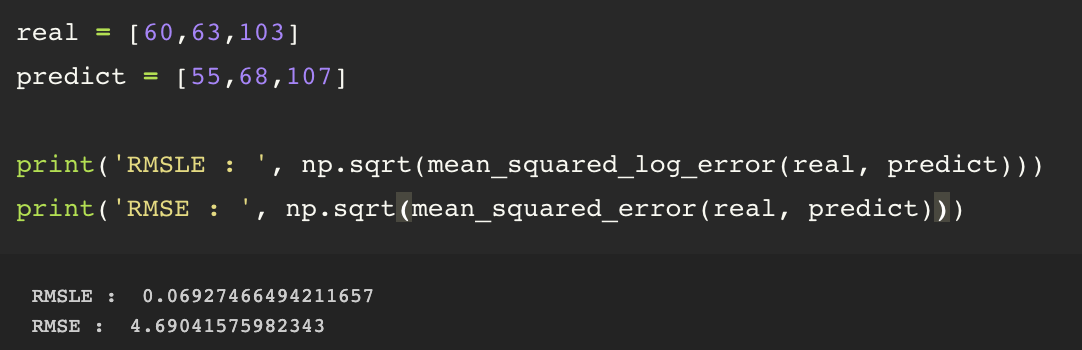
보시는 것과 같이 예측값과 실제값에 이상치처럼 어떤 값이 껴있을 때 RMSE와 RMSLE의 값을보시겠습니다. 그리고 다음은

보시는 것처럼 큰 아웃라이어가 값에 포함되더라도 RMSLE의 값은 거의 변화가 없지만 RMSE는 변화폭이 큰 것을 볼 수 있습니다. 따라서 RMSLE는 RMSE에 비해 아웃라이어에 강한 것을 알 수 있습니다.

 

두번째로 2. 과소평가된 항목에 큰 패널티를 부여한다 입니다.

 

과소평가 된 항목에 큰 패널티를 줌으로써 예측시 실제값과 같은 폭의 오차를 보이더라도 예측값의 성격에 따라서 다른 척도를 보여준다는 것입니다. 과소평가 즉, 실제값보다 작은 값으로 예측했을 때 RMSLE는 큰 값으로 예측했을 때보다 더 높은 값을 보입니다. 설명이 이해되지 않으셨을 것이라 생각되면서 아래의 그림을 보시겠습니다.

보시는 것처럼 실제값과 예측값 사이에 같은 폭의 오차를 보이더라도 RMSE는 같은 값은 항상 반환하는 반면, RMSLE는 예측값이 실제값보다 작게 예측이 되었을 때 그에 대해서 패널티를 더 부여하여 마치 "너 제대로 예측해"라는 것처럼 성능을 안좋게 판단하여 반환합니다.

예를 들어서 수요량을 예측하여 모든 소비자들이 구매할 수 있도록 할 때 수요량을 10명이라고 예측해서 8명의 사람들이 구입을 해서 2개가남 는 경우가 수요량을 10명이라고 예측해서 12명의 소비자들이 구매하려고 해서 2명의 소비자들이 구매를 하지 못하는 경우보다 낫기 때문에

RMSLE는 과소평가 항목에 더 패널티를 줘서 이와 같은 문제점을 보완해주는 강점을 가지고 있습니다.

 

마지막으로 3. 상대적 ERROR를 측정해줍니다.

 

RMSE와 다르게 절대적인 값보다 상대적인 값을 파악하여 절대적 오차를 측정하여 반환하는 RMSE와 다르게 상대적 오차를 측정하여 반환해줍니다. 아래의 예를 보겠습니다.

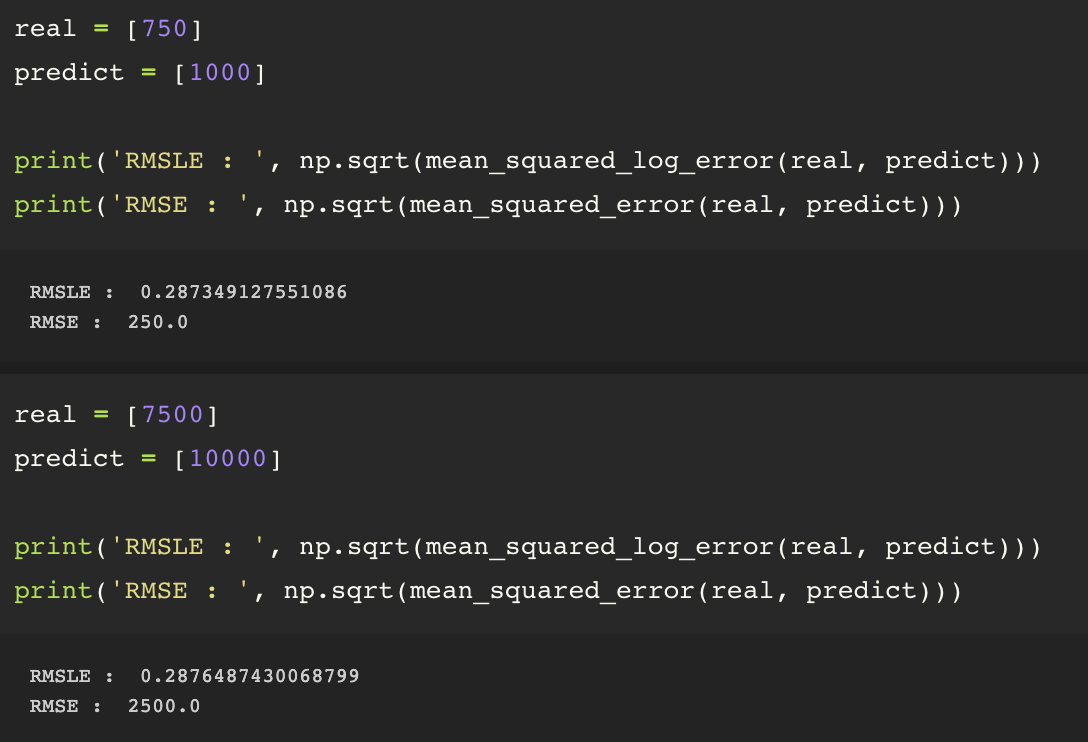
보시는 것과 같이 RMSE는 절대적인 오차가 달라지므로 계속 값이 바뀌지만 RMSLE는 상대적인 비율(오차)가 바뀌지 않으므로 완전 동일한 값은 아니지만 어느정도 동일한 값을 띄는 것을 알 수 있습니다.

 

3. 정리

지금까지 회귀 모델링에서 사용되는 평가 척도와 각 척도의 성격 및 수식 그리고 RMSE와 RMSLE에 대해서 자세히 다뤄봤습니다. 본 포스팅에서 다룬 RMSE vs RMSLE 뿐만이 아니라 다른 척도들도 각각의 장단점을 가지고 있습니다.

앞으로는 분류, 회귀 모델에서 사용하는 지표를 단순히 "A 지표를 사용하니깐 좋더라"가 아니라 "해당 데이터에서는 A 지표보다는 B 지표를 사용하는 것이 OO측면에서 더 낫다" 라고 스스로 생각할 수 있도록 훈련하려고 합니다.

감사합니다.