Machine Learning Imbalanced Data(불균형 데이터)

안녕하세요.

이번에 다룰 내용은 불균형 데이터에 대해서 다뤄보겠습니다.

 

먼저 분류문제를 해결할 때 데이터의 분포를 가장 먼저 확인합니다. 이 때 예측해야하는 결과값의 분포가 100:1, 200:1, 400:1 ... 정도로 굉장히 불균형한 분포를 띄고 있는 데이터들을 많이 만나곤 하는데요. 불균형한 데이터를 그대로 예측하게 과적합문제가 발생할 가능성이 높아집니다.

 

그렇기 때문에 예측시 이러한 과적합 문제를 해결하기 위해서는 다양한 방법론이 있지만 기본적으로 데이터가 불균형하다면 불균형 문제를 해결한 뒤 문제에 접근을 해야합니다.

 

여담으로 최근에 참여했던 프로젝트에서 데이터의 불균형성을 인지하고 있지만 해결하지 않아서 Public Score와 Local 예측값과의 차이가 심하게 났던 과적합을 일으켰으며, 불균형 문제를 해결했을 때의 결과와 많은 차이를 보였던 경험이 있습니다. boosting모델 자체에서 class_weight = 'balanced' 를 통해서 어느정도 불균형 문제를 해결하려했고, 불균형 분포 차이가 1 : 0.04 였기 때문에 샘플링을 했을 때 발생할 수 있는 편향성 문제가 더 클 것이라고 예상했기 때문에 따로 샘플링 과정을 거치지 않았는데 거기서 문제가 발생했었습니다. 그래서 최종적으로 본선은 진출했지만 입선에 그치게 되었는데요. 이처럼 피부로 문제를 느껴보니 이부분에 대해서 한번 짚고 넘어갈 필요가 있다고 생각하게 되었습니다

 

1. 정의

데이터가 불균형하다는 말이 어떤 뜻일까요?

남/여, 구매여부 등 클래스 분포를 예측해야 하는 분류문제에서 예측 라벨 값의 분포가 100:1, 200:1 등으로 불균형하게 나타나는 상태를 말합니다. 아래의 그래프를 보시겠습니다. 

 

 

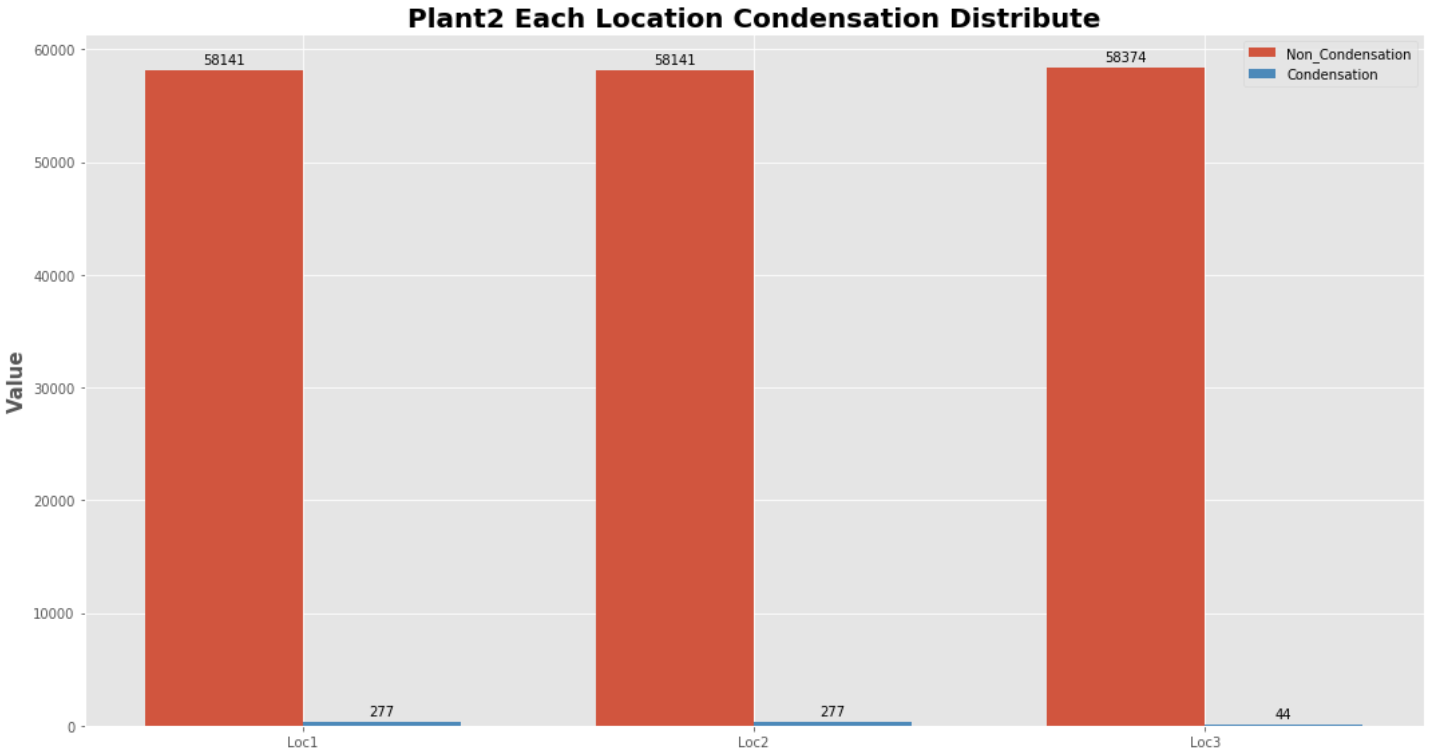
위의 그래프는 결로현상을 예측해야하는 문제에서 결로현상(라벨 값)의 분포를 나타낸 것인데요. 보시는 것처럼 굉장히 불균형한 상태인 것을 알 수 있습니다. 저희는 이러한 문제를 해결하기 위해서 이제부터 소개할 일련의 과정들을 거쳐야 할 것입니다.

 

 

 

2. 불균형으로 발생하는 문제

불균형 데이터 상태 그대로 예측하게 된다면 위에서 말씀드린대로 과적합 문제가 발생할수 있습니다. 대표적으로 과적합은 변수가 많아서 생기는 모델 복잡성 증가, 데이터 불균형으로 생기는 문제 등의 다양한 발생 원인들이 존재하지만 이번 포스팅에서 소개해드릴 내용은 데이터 불균형으로 발생하는 과적합에 대해서 설명드리겠습니다.

 

데이터가 불균형하다면 분포도가 높은 클래스에 모델이 가중치를 많이 두기 때문에 모델 자체에서는 "분포가 높은 것으로 예측하게 된다면 어느정도 맞힐 수 있겠지?"라고 생각합니다. 따라서 불균형 문제를 해결하지 않으면 모델은 가중치가 높은 클래스를 더 예측하려고 하기 때문에 Accuracy는 높아질 수 있지만 분포가 작은 값에 대한 Precision은 낮을 수 있고, 분포가 작은 클래스의 재현율이 낮아지는 문제가 발생할 수 있습니다.

 

"예를들어서 분포가 100개의 데이터에서 1과 0값이 각각 97 : 3 비율을 가지고 있을 때 모든 값을 1로 예측한다 하더라도 정확도가 97% 나오게 됩니다."

 

그리고 Train Set에서는 높은 성능을 보이지만 새로운 데이터 혹은 테스트 데이터에서는 예측 성능이 더 낮을 수 있습니다.

저희가 항상 모델을 만들 때 일반화 정도가 높은 모델을 만드는 것이 중요한데(어떠한 데이터에서도 비슷한 성능을 보여주는 모델) 과적합 문제는 이러한 부분을 즉, 일반화 정도를 낮출 수 있으므로 불균형 문제를 해결하는 것이 굉장히 중요하다고 할 수 있습니다.

 

자, 그러면 데이터 불균형성을 해결할 수 있는 방법론은 어떤 것이 있을까요?

 

3. 데이터 불균형성 해결 방법론

해결 방법론으로는 1. Under Sampling 2. Over Sampling 3. Data argumentaion(불균형 문제와는 좀 다른 부분이긴 합니다.) 이 존재합니다. 먼저 Under Sampling, Over Sampling에 대해서 살펴보겠습니다.

 

3-1. Under Sampling

Under Sampling은 Down Sampling라고도 불리며 데이터의 분포가 높은 값을 낮은 값으로 맞춰주는 작업을 거치는 것을 말합니다.

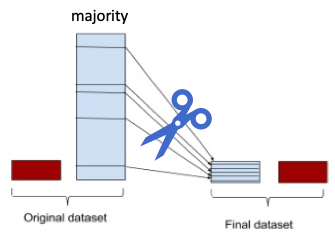
위의 그림처럼 데이터 분포를 확인한 후 분포가 높은 class를 낮은 분포의 class 크기에 맞춰주는 작업을 거칩니다.

 

이러한 과정을 거치면

 

장점으로는 유의미한 데이터만을 남길 수 있습니다

단점으로는 정보가 유실되는 문제가 생길 수 있습니다.

 

이제 Under Sampling 방법론 몇가지를 소개하겠습니다.

 

 

3-1.1. Random Under Sampling

말그대로 무작위 샘플링을 하는 방법인데요.

먼저 해결해야하는 불균형 데이터의 분포를 보겠습니다.

해당 9:1 데이터를 무작위 샘플링을 적용해 보겠습니다.

 

먼저 불균형 데이터 샘플을 만들어 보겠습니다.

n0 = 200; n1 = 20
rv1 = sp.stats.multivariate_normal([-1, 0], [[1, 0], [0, 1]])
rv2 = sp.stats.multivariate_normal([+1, 0], [[1, 0], [0, 1]])
X0 = rv1.rvs(n0, random_state=0)
X1 = rv2.rvs(n1, random_state=0)
X_imb = np.vstack([X0, X1])
y_imb = np.hstack([np.zeros(n0), np.ones(n1)])

x1min = -4; x1max = 4
x2min = -2; x2max = 2
xx1 = np.linspace(x1min, x1max, 1000)
xx2 = np.linspace(x2min, x2max, 1000)
X1, X2 = np.meshgrid(xx1, xx2)

def classification_result2(X, y, title=""):
    plt.contour(X1, X2, rv1.pdf(np.dstack([X1, X2])), levels=[0.05], linestyles="dashed")
    plt.contour(X1, X2, rv2.pdf(np.dstack([X1, X2])), levels=[0.05], linestyles="dashed")
    model = SVC(kernel="linear", C=1e4, random_state=0).fit(X, y)
    Y = np.reshape(model.predict(np.array([X1.ravel(), X2.ravel()]).T), X1.shape)
    plt.scatter(X[y == 0, 0], X[y == 0, 1], marker='x', label="0 클래스")
    plt.scatter(X[y == 1, 0], X[y == 1, 1], marker='o', label="1 클래스")
    plt.contour(X1, X2, Y, colors='k', levels=[0.5])
    y_pred = model.predict(X)
    plt.xlim(-4, 4)
    plt.ylim(-3, 3)
    plt.xlabel("x1")
    plt.ylabel("x2")
    plt.title(title)
    return model

 

그 다음 해당 불균형 데이터 셋을 무작위 언더 샘플링 과정을 통해서 균형있는 데이터 셋으로 변경해보겠습니다.

 

X_samp, y_samp = RandomUnderSampler(random_state=0).fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)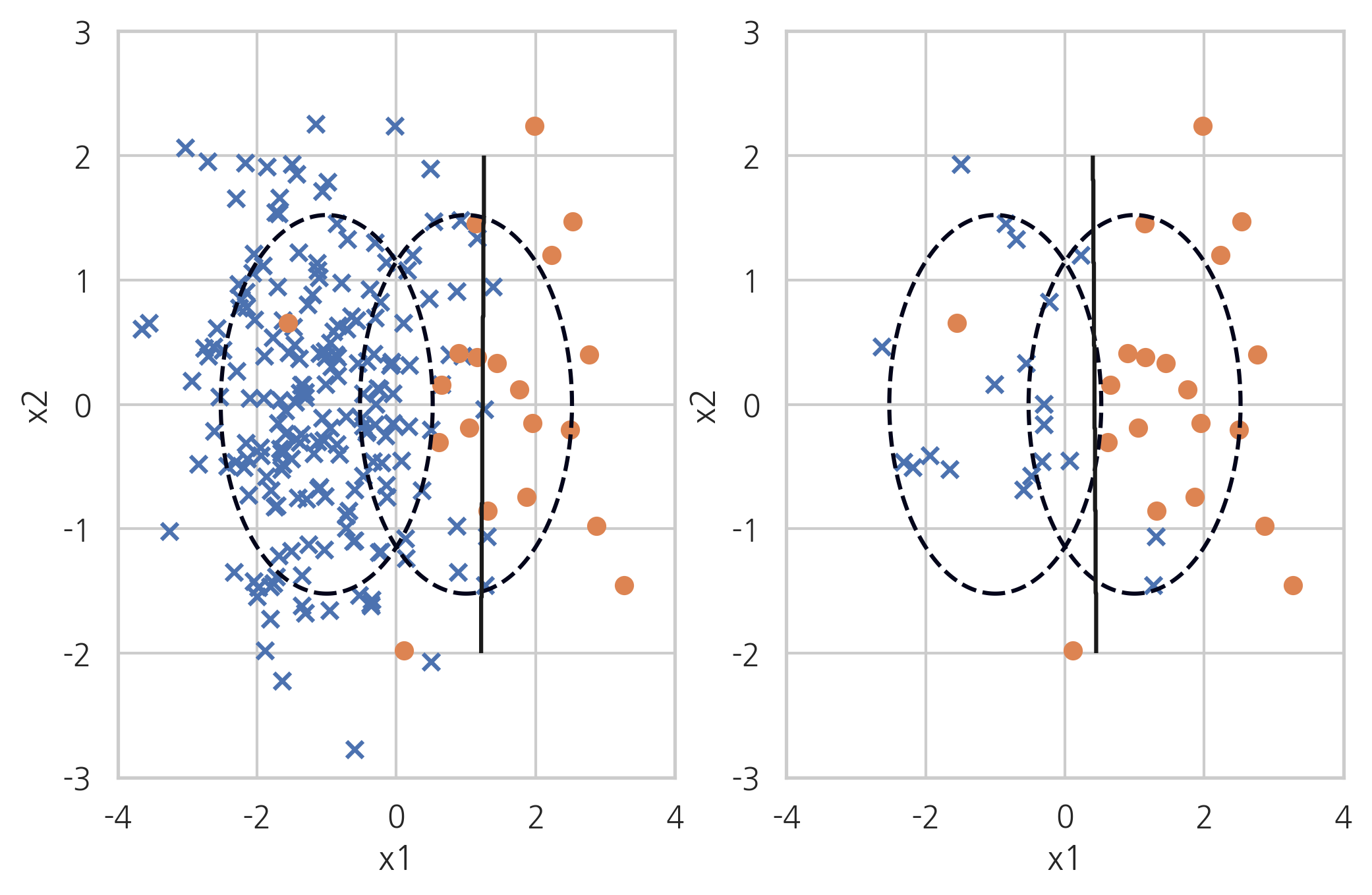

 

무작위 랜덤 샘플링 과정을 거치면 위와 같은 그림이 나오게 됩니다. 분포가 높은 클래스의 값을 어떠한 조건 없이 무작위로 삭제하는 과정이며 이와 같은 과정을 통해서 분포가 낮은 클래스의 데이터 크기와 맞출 수 있게 됩니다.

어떠한 조건 없이 데이터 분포를 맞추는 것이기 때문에 걸리는 시간이 굉장히 빠른 장점이 있습니다.

 

3-1.2. Tomek link

토멕링크 방법론은 분포가 작은 클래스의 데이터에서 가장 가까운 분포가 높은 데이터의 위치를 찾는 것입니다. 즉, 서로 다른 클래스가 있을 때 서로 다른 클래스끼리 가장 가까운 데이터들이 토멕링크로 묶여서 토멕링크 중 분포가 높은 데이터를 제거하는 방법론입니다.

토멕링크를 찾아서 제거하는 방법론이기 때문에 클래스를 나누는 TreshHold를 분포가 높은 쪽으로 밀어 붙이는 효과가 있습니다. 

X_samp, y_samp = TomekLinks().fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)

 

Tomek link는 분포가 높은 클래스의 중심분포는 어느정도 유지하면서 경계선을 조정하기 때문에 무작위로 삭제하는 샘플링보다 정보의 유실을 크게 방지할 수 있지만 토멕링크로 묶이는 값이 한정적이기 때문에 큰 언더 샘플링의 효과를 얻을 수 없다는 단점이 있습니다.

 

3-1.3. CNN(Condensed Nearest Neighbour)

CNN 방법은 최근접인 클래스 분포 데이터를 삭제하면서 샘플링하는 방법론입니다.

 

1. 분포가 작은 클래스르 S분포로 둡니다.

2. 분포가 큰 클래스를 랜덤으로 하나 선택한 뒤 그 데이터 위치에서 가장 가까운 데이터를 선택했을 때 S 분포에 포함 되어 있지 않은 데이터라면 제거합니다.

3. 가장 가까운 값이 S분포가 나올 때까지 2번을 반복합니다.

 

X_samp, y_samp = CondensedNearestNeighbour(random_state=0).fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)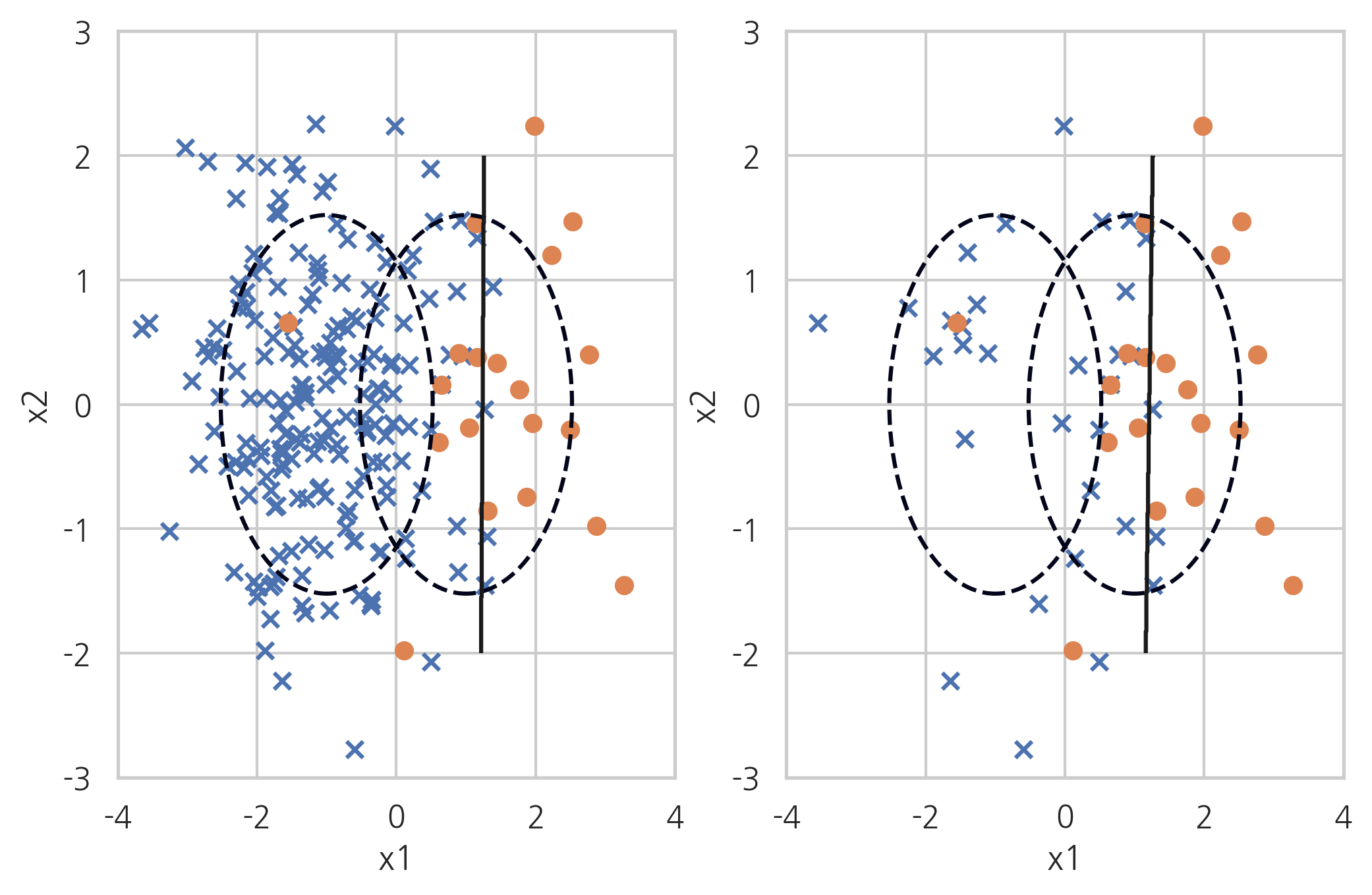

 

 

이 과정을 거치면 분포가 큰 클래스 값을 효율적으로 제거할 수 있게 됩니다.

 

위의 Tomek link 방법론과 CNN방법론을 합쳐서 만든 One sided Selection 방법론이 있는데 토멕링크로 먼저 데이터를 제거한 후 분포가 큰 클래스 내부에서 CNN방법으로 데이터를 데이터를 제거하는 과정을 거치는 방법입니다.

 

X_samp, y_samp = OneSidedSelection(random_state=0).fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)

 

3-1.4. Edited Nearest Neighbours

ENN방식은 KNN방식이랑 비슷하며 소수 클래스 주변의 다중 클래스 값을 제거하는 방법론입니다. 해당 방법론은 토멕링크 방법론 처럼 클래스를 구분하는 임계점을 다중 클래스 쪽으로 밀어낼 수 있지만 제거 효과가 크지 않은 것을 알 수 있습니다.

 

X_samp, y_samp = EditedNearestNeighbours(kind_sel="all", n_neighbors=5, random_state=0).fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)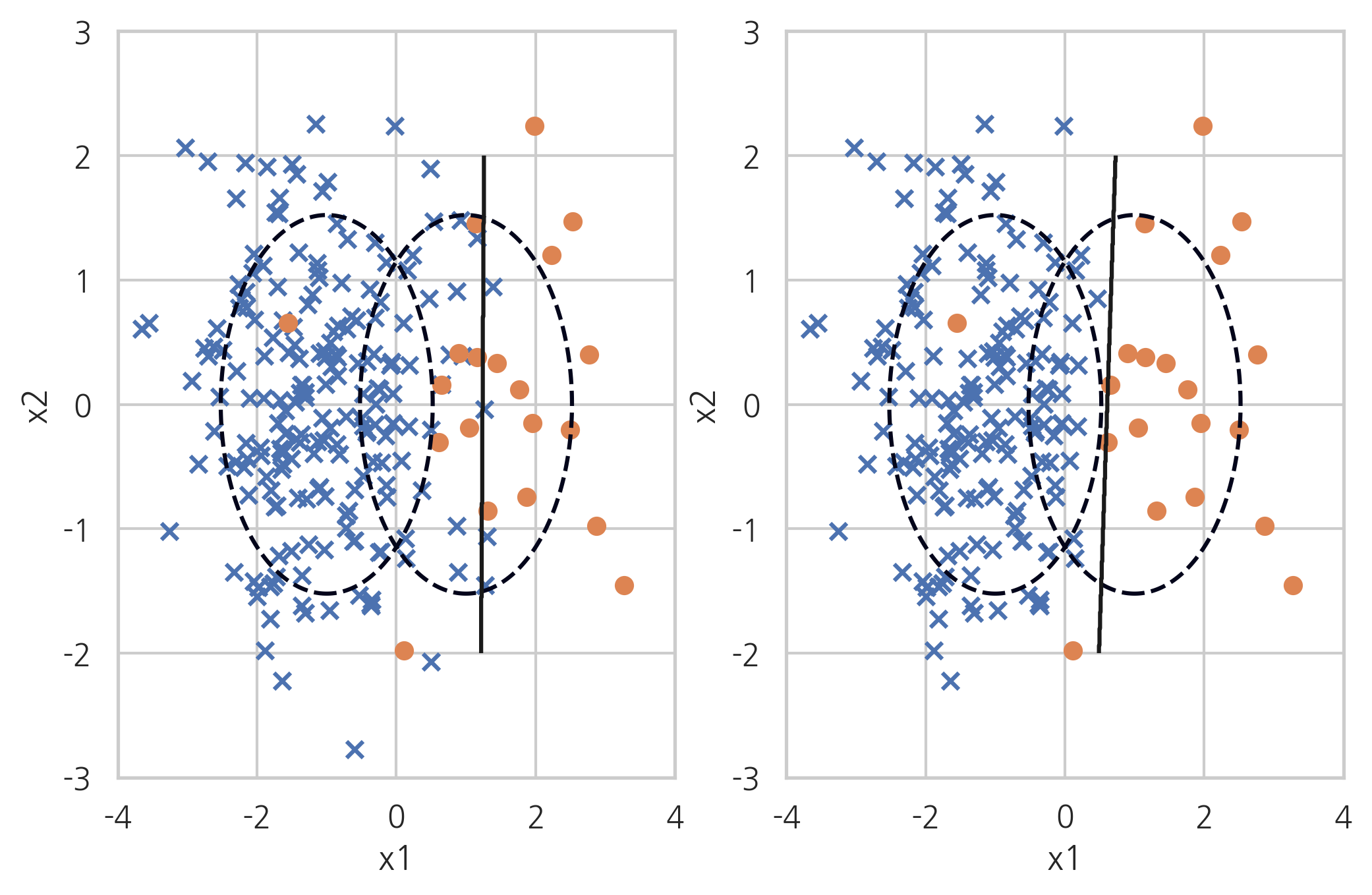

 

마지막으로 CNN방법과 ENN방법을 섞은 Neighbourhood Cleansing Rule가 있습니다. 분포가 큰 데이터에 대한 제거 효과가 크지 않지만 좀 더 직관적으로 두 클래스를 나눌 수 있는 장점이 있습니다.

 

X_samp, y_samp = NeighbourhoodCleaningRule(kind_sel="all", n_neighbors=5, random_state=0).fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)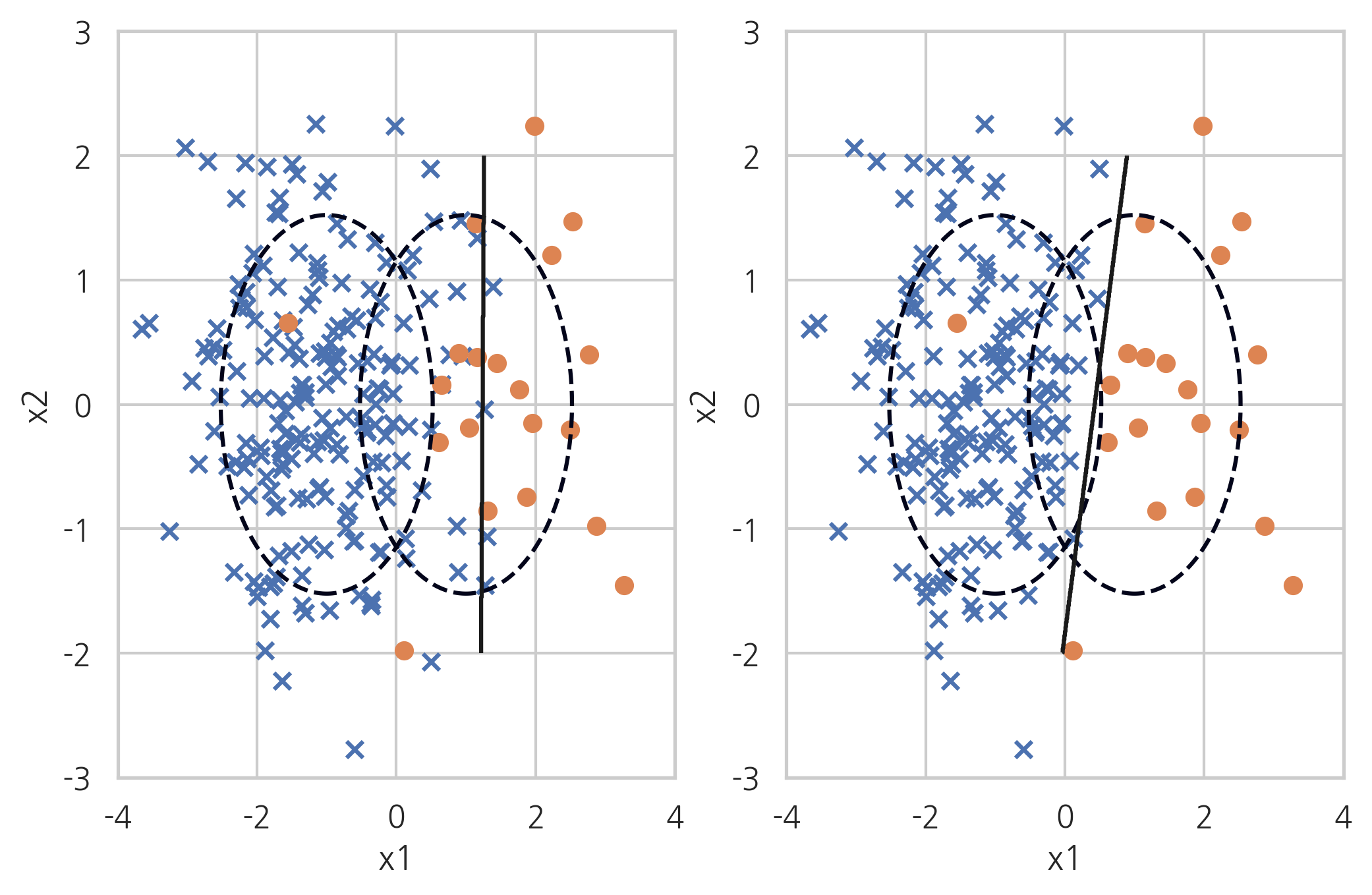

 

3-2. Over Sampling

오버 샘플링은 Up Sampling라고도 불리며 분포가 작은 클래스의 값을 분포가 큰 클래스로 맞춰주는 샘플링 방법입니다.

위의 그림을 통해서 알 수 있듯이 분포가 작은 클래스 값을 일련의 과정을 거쳐 생성하는 방법을 뜻합니다.

이와 같은 과정을 거치게 되면

 

장점으로는 정보의 손실을 막을 수 있다

단점으로는 여러 유형의 관측치를 다수 추가하기 때문에 오히려 오버피팅을 야기할 수 있습니다.

 

따라서 새로운 데이터, Test 데이터에서의 성능이 나빠지는 결과를 초래할 수 있습니다.

 

3-2.1. Random Over Sampling

무작위로 분포가 작은 클래스의 데이터를 생성하는 것을 말합니다. 즉, 소수의 클래스 데이터를 반복해서 넣는 것으로 가중치를 증가시키는 것과 비슷합니다.

 

X_samp, y_samp = RandomOverSampler(random_state=0).fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)

무작위로 소수 클래스의 데이터를 반복해서 집어넣는 방법이기 때문에 반복 데이터 삽입으로 인한 오버피팅 문제가 발생할 수 있습니다.

 

3-2.2. ADASYN(Adaptive Synthetic Sampling) 

ADASYN방법론은 분포가 작은 클래스 데이터와 그 데이터와 가장 가까운 무작위의 K개의 데이터 사이에 가상의 직선을 그려서 직선상에 존재하는 가상의 분포가 작은 클래스 데이터를 생성하는 것을 말합니다.

 

X_samp, y_samp = ADASYN(random_state=0).fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)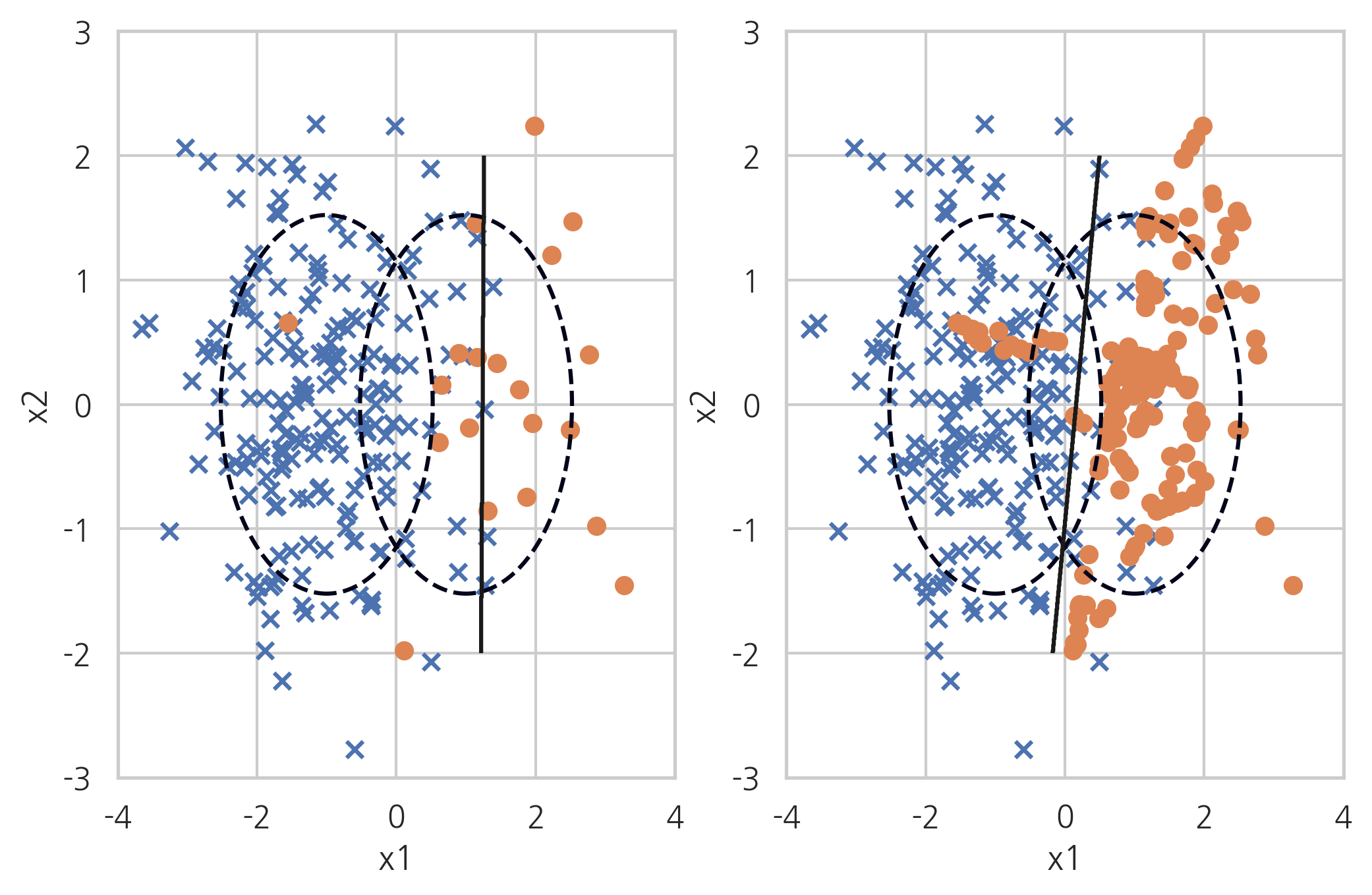

 

해당 방법론을 통해서 단순 무작위 오버샘플링으로 인해 발생하는 과적합 문제를 해결할 수 있습니다. 단순 오버 샘플링은 데이터를 무작위로 가중치를 기반하여 복제하는 것이기 때문에 해당 방법론을 통한 오버샘플링이 좀 더 나은 방법론이라고 말 할 수 있을 것 같습니다. 단점으로는 시간이 좀 걸리는 문제가 있습니다.

 

3-2.3. SMOTE

SMOTE는 ADASYN과 같은 방법론으로 데이터를 생성하지만 생성된 데이터가 분포가 적은 클래스에 포함되는 것이 아니라 분류 모형에 따라서 다르게 분류합니다.

 

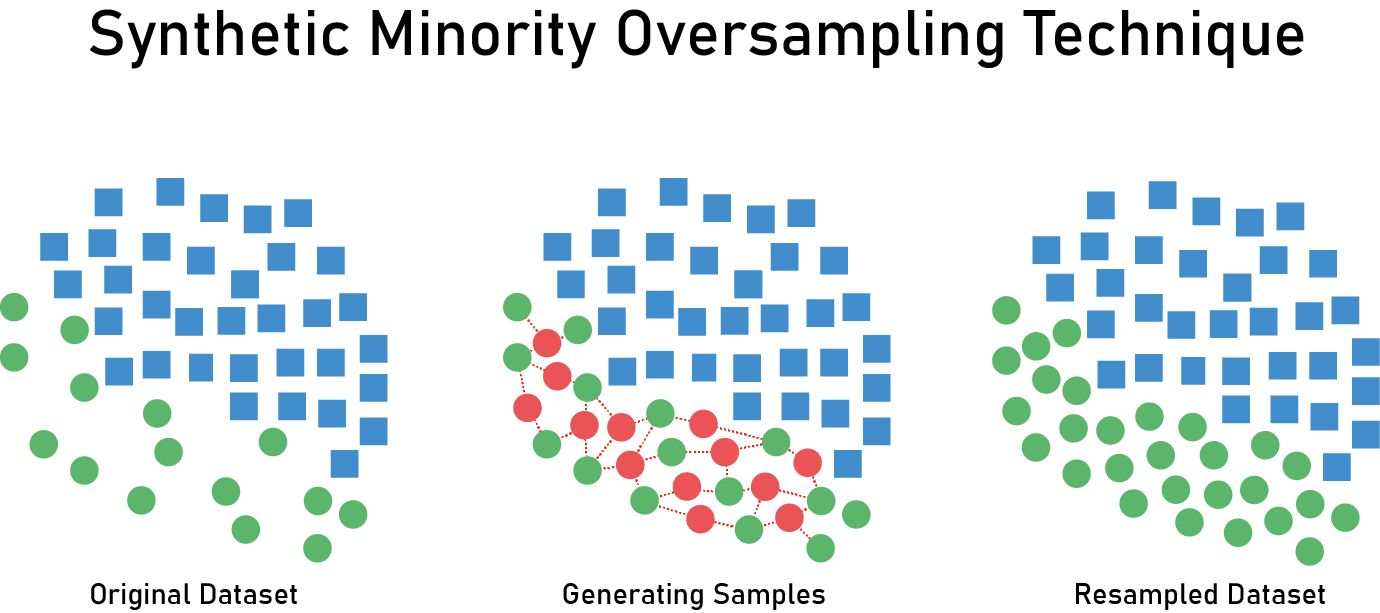
X_samp, y_samp = SMOTE(random_state=4).fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)

 

3-3. Combine Sampling

복합 샘플링은 오버샘플링과 언더샘플링을 결합한 샘플링 방법론으로 두가지의 종류가 있습니다.

 

3-3.1. SMOTE + ENN

SMOTE와 ENN방법론을 결합한 방식입니다

X_samp, y_samp = SMOTEENN(random_state=0).fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)

 

 

3-3.2. SMOTE + TOMEK

SMOTE와 TOMEK방법론을 결합한 방식입니다.

X_samp, y_samp = SMOTETomek(random_state=4).fit_sample(X_imb, y_imb)

plt.subplot(121)
classification_result2(X_imb, y_imb)
plt.subplot(122)
model_samp = classification_result2(X_samp, y_samp)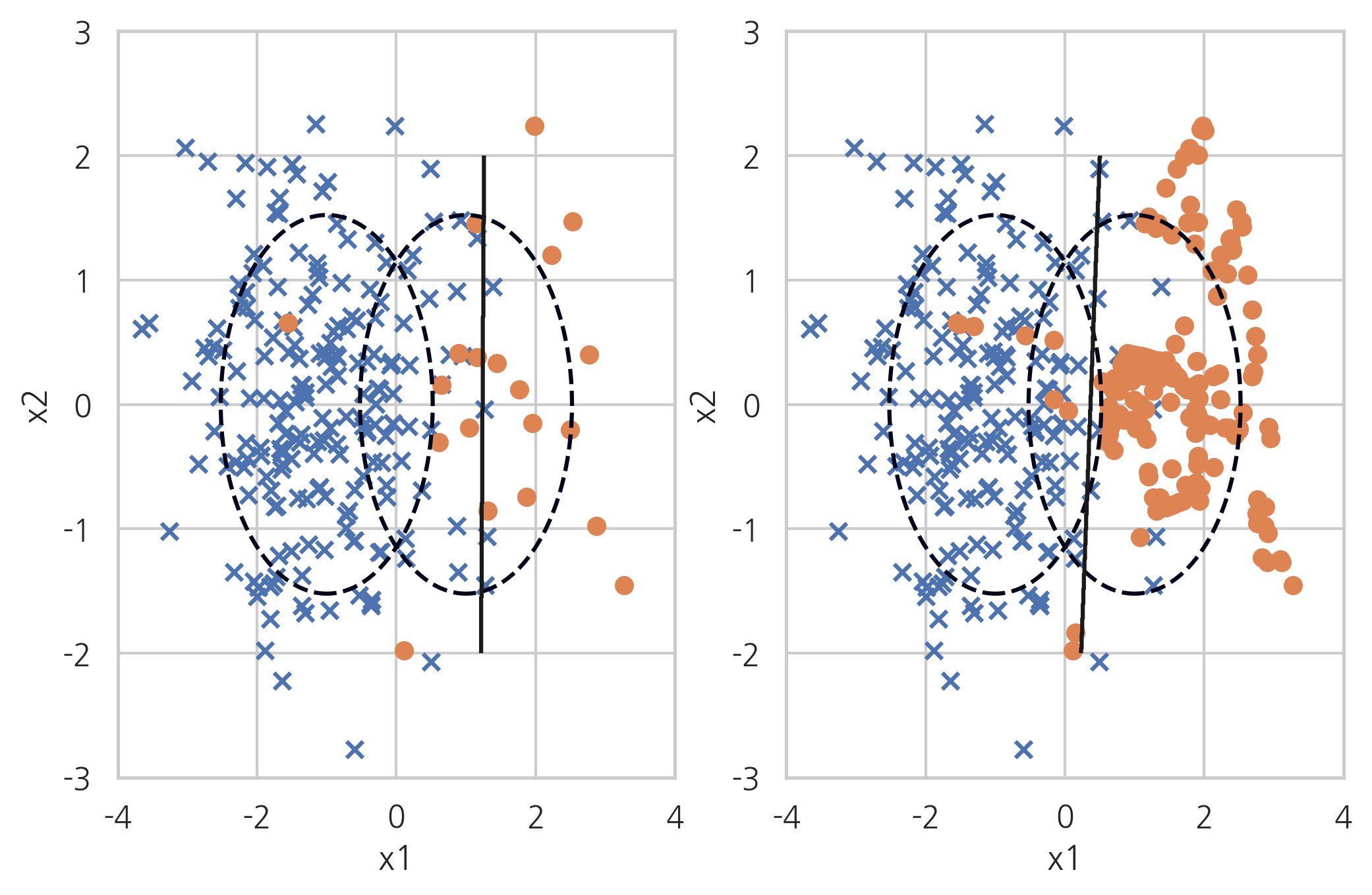

 

번외) Data Argumentation

 

Data Argumentation은 주로 이미지 분석에서 사용되는 방법론으로 불균형 데이터 상태에서 방법론으로 사용되는 오버샘플링과 데이터를 생성하거나 증가시키는 원리는 비슷하지만 다른 부분이 존재합니다. 따라서 이부분은 추후에 자세히 다룰 내용이며 불균형 데이터 셋을 처리하는 방법론 외의 번외 부분으로 봐주시면 감사하겠습니다!

 

Data Argumentation은 이미지 분석에서 Over fitting을 방지하고 예측에 대한 신뢰성을 높이기 위한 추가적인 데이터를(이미지) 생성하는 방법론입니다. 따라서 이부분은 GAN으로 데이터를 generate하는 방식과 거의 비슷하다고 보시면 되겠습니다. 그림으로 보시면 편할텐데요

 

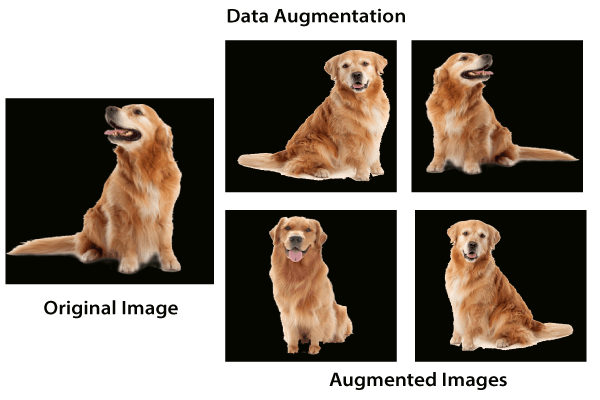
위와 같이 하나의 이미지를 가지고 다양한 구도와 각도로 새롭게 생성과정을 거치는 것이 Data Argumentation의 기본 개념입니다. 이 부분은 추후 포스팅에서 자세히 다뤄보겠습니다!!

 

 

 

이렇게 불균형 데이터 상태에서 처리할 수 있는 다양한 샘플링 기법들을 소개해드렸는데요. 저는 직접 불균형 데이터셋을 처리하지 않은 상태로 분석을 진행하여 좋지 못한 성능을 낸 경험을 몸소 느꼈기 때문에 불균형 데이터에 대한 처리 즉, 보간법에 대한 중요성을 배우게 되었습니다. 해당 포스팅을 보시는 데이터 분석에 관심을 가지고 계시거나, 관련 프로젝트를 진행하고 계시는 분들께서는 불균형 데이터에 대해서 좀 더 엄격하게 바라보는 시각이 필요할 것이라고 생각됩니다!

 

" 정조曰 모든 일에는 기본이 중요하다"

 

위의 말에서 느낄 수 있듯이 분석을 할 때도 기본에 충실한 분석을 진행해야 시작부터 결과까지의 과정이 탄탄하게 이뤄질 수 있다고 생각합니다. 기본에 충실한 분석가를 위해서 한걸음 한걸음 같이 나아갔으면 하는 바램입니다! 

 

참고

https://datascienceschool.net/view-notebook/c1a8dad913f74811ae8eef5d3bedc0c3/