-
AUC와 ROC CurveStatistics 2020. 4. 15. 18:26
안녕하세요
이전 포스팅에 이어서 AUC와 ROC Curve에 대해서 살펴보고자 합니다.
본 포스팅에 앞서 이전에 학습했던 것을 살짝 언급해보면 분류 모델의 성능을 평가하는 척도로는 Accuracy, AUC, F1 Score 등을 많이 사용하고 있습니다.
이와 같은 지표들을 어떻게 산출할까요? 바로 Confusion Matrix(혼돈행렬)에서 지표를 추출합니다.

위에 보시는 그림이 Confusion Matrix를 간략하게 그려본 것인데요.
이를 통해서
- Accuracy
- Sensitivity
- Precision
- Specificity
- F1 Score
- Error Rate
의 지표를 추출할 수 있습니다. 위 지표들에 대한 자세한 설명은 아래의 글을 참고해주세요.
Confusion Matrix의 손쉬운 이해
안녕하세요. 이번엔 봐도봐도 항상 헷갈릴 수 있는 Confusion Matrix 부터 AUC, ROC Curve에 대해서 설명해드리고자 합니다. 저희는 어떤 미지의 값을 예측할 때 예측에 대한 성능을 다양한 척도(Metric)로 평가하..
shinminyong.tistory.com
그럼 본격적으로 AUC란 무엇이고, ROC Curve는 무엇을 뜻하는지 알아보겠습니다.
AUC, ROC Curve
일단 AUC를 알기 위해서는 True Positive Rate인 Sensitivity와 True Negative Rate인 Specificity를 파악해야 합니다.
앞서, Sensitivity는 행방향이며 실제 환자를 잘 예측한 비율을 나타냅니다. 공식은 아래와 같습니다.
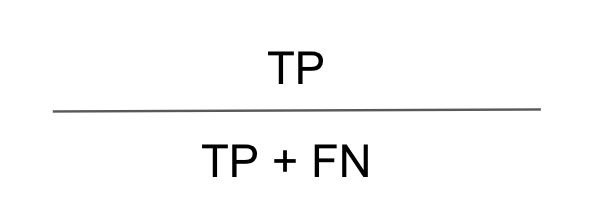
그리고 Specificity은 마찬가지로 행방향이며 얼마나 비환자를 잘 예측했는지를 비율로 나타냅니다. 공식은 다음과 같습니다.
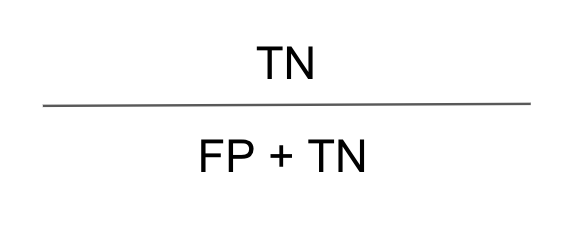
이렇게 두개의 지표를 잘 이해했다면 AUC에 대해서 생각하는데 큰 무리가 없을겁니다.
먼저 이 두 지표의 분포도를 그려보겠습니다.

분포도에서 연한 파란색 부분이 Specificity, 연한 연두색 부분이 Sensitivity를 나타냅니다.
그리고 중간에 Decision threshold부분이 Cutoff를 뜻하며 기준이 되는 임계치 나타냅니다. 즉, 임계치를 어떻게 설정하는지에 따라서 민감도와 특이도의 값이 달라질 수 있습니다.
아래의 그림을 보시겠습니다.

위의 분포도를 해석해보자면 기준 Cutoff(임계점) (3)에서 낮게 잡을수록 True Positive Rate가 높아집니다. 즉, 환자라고 예측하는 것이 많아지므로 Sensitivity(민감도)가 점차 증가하는 것을 알 수 있습니다. 그러면서 환자라고 예측하는 것이 많아지므로 False Positive Rate도 같이 증가하며 반대로 True Negative Rate는 점차 낮아지게 됩니다.
그리고 기준 임계점을 점점 높게 잡을수록((6)으로 갈수록) 환자라고 예측하는 비율이 적어져 True Positive Rate(Sensitivity)가 감소하게 됩니다. 그러면서 True Negative Rate(Specificity)는 점차 증가하게 됩니다.
분포도를 확인해보면 항상 환자를 예측하는 것, 비환자를 예측하는 것 사이에는 Error를 교집합으로 포함하고 있기 때문에 아무리 최선의 Cutoff를 찾았다고 하더라도 오차를 포함하는 값을 도출할 수밖에 없게 됩니다. 하지만 분포도에서 겹치지 않는 분포를 가지고 있는 데이터가 있다면 정확히 분류를 할 수 있어 Error가 적은 최적의 ROC Curve를 찾을 수 있게 됩니다.
그럼 직접 ROC Curve를 그려 설명해보겠습니다.

AUC는 [0,1]의 범위를 같는데요. 위에서 언급한 것처럼 환자 예측 분포, 비환자 예측 분포도의 겹치는 부분이 많다면 높은 AUC를 도출하지는 못할 수 있습니다. 이유는 말씀드렸다시피 예측과 실제 값에서 생기는 오차 때문인데요. 만일 겹치는 부분이 많이 없다면 오차가 적을테니 높은 AUC를 도출할 수 있을 것입니다.
그래서 일반적으로 AUC는 높을수록 좋은 성능의 척도로써 사용되며, 높은 AUC가 높을수록 최적의 분류모델을 나타낸다고 할 수 있습니다.
극단적으로 생각해보면서 임계치를 분포도 왼쪽 끝까지 당겨보겠습니다. 그러면 모두 환자라고 예측하는 모델이 만들어지겠죠?
그러면 지표들의 값은 어떻게 나타나게 될까요?
모두 환자라고 예측하므로 Specificity가 0이 되고, Sensitivity가 1이 될 것입니다. 그러면 FPR값도 1이 되어 ROC Curve그래프를 보면 x값과 y값이 1과 1에서 만나는 것을 확인할 수 있습니다.
반대로 오른쪽 끝가지 당겨보겠습니다. 이제 어떤 지표값이 도출될지 감이오시나요?
모두 환자가 아니다라고 예측하여 TPR과 FPR값이 0이 나오게 됩니다.
다시 복습해보면 임계점을 낮출수록 환자라고 예측하는 비율이 높아지기 때문에
True Positive Rate가 증가 / False Positive Rate가 증가 / True Negative Rate가 감소
이를 종합해보면 TPR은 FPR과 비례관계, TNR과는 반비례 관계임을 알 수 있습니다.
결론
여기까지 공부하다보면 "그럼 환자인 것을 예측하는 TPR과 FPR이 같이 높아지는 것이 좋은 것 아닌가?", "그러니까 임계점을 최대한 낮게 잡아서 TPR을 높이는 방향이 좋지 않을까?" 라는 생각이 들 수 있습니다.
결론적으로 틀린 말은 아니지만 어떤 데이터를 분석하는지, 예측하는 값이 결과 값에 얼마나 민감한지에 따라서 적절하게 선택해야 한다는 것입니다. 예로 들어보겠습니다.
"여기 A라는 의사가 있습니다. 해당 의사는 암 환자를 검진하는 전문의로써 환자들의 암 진단 여부를 확실히 해야하는 막중한 책임을 안고 있습니다. 암은 알다시피 걸릴 확률은 적지만 높은 치사율을 가지고 있습니다. 의사입장에서는 암환자를 찾는 것이 중요할까요? 암환자가 아닌 사람을 찾는 것이 중요할까요?"
"두번째 B라는 의사가 있습니다. 이 의사는 일반 내과에서 일하는 의사로 주로 알레르기성 비염, 감기 환자들을 많이 상대하고 있습니다. 감기와 비염은 걸릴 확률은 높지만 치사율은 극히 적습니다. 그러면 이 의사는 해당 병을 진단하는 것이 중요할까요? 해당 병이 아니라는 것을 진단하는 것이 중요할까요?"
위의 첫번째 예시에서 치사율이 높은 위험한 병은 최대한 환자임을 예측하여 환자가 아닌데 환자라고 오진을 받은 환자가 많더라도 실제 환자를 환자라고 예측하는 것이 중요하다고 할 수 있습니다. 두번째 예시는 반대의 결과지만 비슷한 케이스라고 볼 수 있습니다.
따라서 분류문제에서 무조건 Accuracy로만 좋은 모델의 성능을 평가하기에는 한계가 있습니다. 데이터마다 가지고 있는 클래스 분포, 상황에 따라서 다양한 지표들을 같이 고민해봐야 하는데 그 중 하나가 AUC로 평가 척도를 검증하는 것입니다. 즉, Cutoff(임계점, Decision point)에 따라 민감하게 움직이는 지표를 안정적으로 검증할 수 있는 것입니다.
'Statistics' 카테고리의 다른 글
Machine Learning Imbalanced Data(불균형 데이터) (1) 2020.07.25 Classification Evaluation Metric (0) 2020.07.12 Regression Evaluation Metric (2) 2020.07.05 Confusion Matrix의 손쉬운 이해 (3) 2020.04.12