하이퍼 파라미터 Bayesian Optimize

1. 들어가며

베이지안 최적화(Bayesian Optimize)를 통한 하이퍼 파라미터 최적화 방법을 소개해드리겠습니다.

 

요즘 대회들을 많이 참가하면서 모델 선택 및 Feature engineering이 어느정도 마무리 된 후에 하이퍼 파라미터 최적화 단계에서 어떻게 하면 적절한 파라미터를 선택할 수 있을지에 대한 고민을 많이 가지고 있습니다.

 

그래서 다양한 파라미터 최적화 방법중에 bayesian optimization에 대해서 소개해드리겠습니다. 먼저 하이퍼 파라미터 최적화 방법론에 대해서 알아보겠습니다.

 

• RandomGrid Search
• Manual Search
• Random Search
• Grid Search
• Bayesian Search

위와 같이 다양한 최적화 방법론이 존재하고 있는데 이중에서 어떤것을 사용하면 적절한 파라미터를 최적화 할 수 있을지에 대해서 고민도 될 것입니다. 물론, 위의 방법론을 모두 사용하여 도출되는 파라미터를 비교하고 각기 다른 파라미터들로 학습한 모델들끼리의 앙상블을 하거나, 가장 성능이 좋은 파라미터를 사용할 수도 있을 것입니다. 하지만 대회에 참여하다보면 항상 시간이 부족하기 때문에 가장 최선의 방법론을 이용하여 빠르게 탐색하는 것이 중요할 수 있습니다. 따라서 위의 방법론들은 추후 포스팅에서 모두 다루겠지만 이번에는 베이지안 최적화를 통해서 비교적 빠르고 쉽게 파라미터를 찾아서 모델에 활용할 수 있는 방법을 소개해드리겠습니다.

 

2. 베이지안 최적화란?

베이지안 최적화는 알려져 있지 않은 목적함수를 최대화(혹은 최소화)로 하는 최적해를 찾는 기법으로 지금까지 확보된 데이터화 평가지표의 숨겨진 관계를 모델링하는 Surrogate model과 Surrogate Model를 활용해 다음 탐색지점을 결정하는 Acquisition function으로 구성되어 있습니다. 기본적으로 Surrogate Model은 가우시안 프로세스를 거쳐 만들어지며, Acquisition function은 maximize expected improvement하며 학습이 진행됩니다.

 

 

3. 왜 베이지안 최적화?

베이지안 최적화는 무조건 답이 아니다 라는 것을 먼저 말씀드리겠습니다. 분석가들의 다양한 시각과 경험을 접목시켜 매뉴얼하게 파라미터를 최적화 할 수도 있고, 다양한 샘플들을 추출하여 무작위로 파라미터를 선택하여 결정하는 것이 좋은 방법일 수 있습니다. 더불어 격자탐색, 랜덤탐색 중 효율성과 성능을 동시에 따졌을 때 상대적으로 좋은 성능을 도출하는 알고리즘은 랜덤탐색 방식입니다.

그러면 왜 베이지안 최적화 방식을 사용할까요?

위의 그림처럼 베이지안 최적화 알고리즘은 미지의 목적함수가 최대화 혹은 최소화 되는 매개변수를 찾기 위해서 사전 분포를 활용하게 되는데요. 격자탐색이나 랜덤탐색처럼 모델의 사전분포를 활용하지 않는 것보다 베이지안 최적화를 통해서 사전 분포를 이용하는 것이 더 좋은 성능을 도출하는 매개변수를 찾을 수 있게 됩니다.

 

하지만 베이지안 최적화는 모든 문제에 좋은 성능을 보이는 것은 아니며, 매우 복잡한 문제를 해결하기 위한 일반화된 알고리즘은 아닙니다. 주로 DL보다 ML에서 사용되는 방법론이며 적당한 크기의 하이퍼파라미터와 데이터 수를 가지고 있을 때 최적화되어 있습니다. BO(Bayesian Optimization: BO)는 매개변수를 탐색할 때 기계학습을 이용하는 것으로 ML을 위한 ML입니다. 그럼 다음으로 BO의 성질들을 한번 알아보겠습니다.

 

4. 베이지안 최적화의 일반적인 성질

• 순차적 접근(Sequence access) 방식
• 목적함수의 도함수를 이용하지 않음(posterior)
  • 목적함수의 도함수가 알려져 있지 않기 때문에(그래서 베이지안)
• ML(Surrogant Model)을 활용하여 더 좋은 해가 있는 곳을 예측
  • Surrogant Model의 비용을 최소화 할 수 있는 곳에서 주로 사용
• 목적함수 계산이 크거나 오래걸리지 않는 곳에서 주로 활용(DL에서 잘 사용하지 못하는 이유)
  
  • 목적함수를 계산하는데 들어가는 시간, 기대향상에 들어가는데 걸리는 시간을 적절하게 고려
• 목적함수가 노이즈를 가지고 있을 때 일반적으로 사용

여기서 기대향상을 다음과 같이 정의할 수 있는데 현재까지 추출한 최고 성능의 함수값으로 부터 더 올라갈 수 있는 정도로 정의합니다. 그리고 최고값, 최고의 해를 알고 있으며. 기존의 데이터를 통해서 학습한 모델을 가지고 있는 것을 가정합니다. 그래서 해당 모델이 예측하는 것을 기준으로 학습을 진행하며, 새로운 해를 가정(사전분포)하고 예측값과 분산을 사용자가 가지고 있는 모델로부터 얻어냅니다.(CV도 넣을 수 있음) 마지막으로 예측값과 분산을 바탕으로 기대 향상을 얻어냅니다. 이 때 해당 모델을 Surrogant Model이라고 하는데 정규분포의 밀도함수, 누적함수 등을 활용합니다.

 

그리고 예측같은 경우는 MPI, EI, UCB 방식을 주로 사용하는데 대부분 EI(Expected improvement)를 사용하기 때문에 자세하게는 설명드리지 않겠습니다.

 

5. 베이지안 최적화 예제 코드

이제 마지막으로 모델링 후 베이지안 최적화를 진행할 때 실제로 어떻게 진행되는지 코드를 보여드리겠습니다.

 

먼저 목적함수를 생성합니다. 여기선 lgbm으로 예시를 들고 모델만 적절하게 변화시키면서 사용하시면 됩니다.

#목적함수 생성
def lgbm_cv(learning_rate, num_leaves, max_depth, min_child_weight, colsample_bytree, feature_fraction, bagging_fraction, lambda_l1, lambda_l2):
    model = lgb.LGBMClassifier(learning_rate=learning_rate,
                                n_estimators = 1000,
                                #boosting = 'dart',
                                num_leaves = int(round(num_leaves)),
                                max_depth = int(round(max_depth)),
                                min_child_weight = int(round(min_child_weight)),
                                colsample_bytree = colsample_bytree,
                                feature_fraction = max(min(feature_fraction, 1), 0),
                                bagging_fraction = max(min(bagging_fraction, 1), 0),
                                lambda_l1 = max(lambda_l1, 0),
                                lambda_l2 = max(lambda_l2, 0)
                               )
    scoring = {'roc_auc_score': make_scorer(roc_auc_score)}
    result = cross_validate(model, X, y, cv=5, scoring=scoring)
    auc_score = result["test_roc_auc_score"].mean()
    return auc_score

 

그 다음으로 일반적으로 파라미터 최적화에 사용될 수 있는 파라미터 범위를 설정한 dict 데이터를 준비합니다.

 

pbounds = {'learning_rate' : (0.0001, 0.05),
           'num_leaves': (300, 600),
           'max_depth': (2, 25),
           'min_child_weight': (30, 100),
           'colsample_bytree': (0, 0.99),
           'feature_fraction': (0.0001, 0.99),
           'bagging_fraction': (0.0001, 0.99),
           'lambda_l1' : (0, 0.99),
           'lambda_l2' : (0, 0.99),
          }

 

다음으로 목적함수와 매개변수 범위 설정이 끝났다면 BO 모델을 준비합니다.

 

lgbmBO = BayesianOptimization(f = lgbm_cv, pbounds = pbounds, verbose = 2, random_state = 0 )

 

모델이 준비되었으면 이제 목적함수가 최대가되는 최적해를 찾으면 됩니다.(acq = ei)

 

lgbmBO.maximize(init_points=5, n_iter = 20, acq='ei', xi=0.01)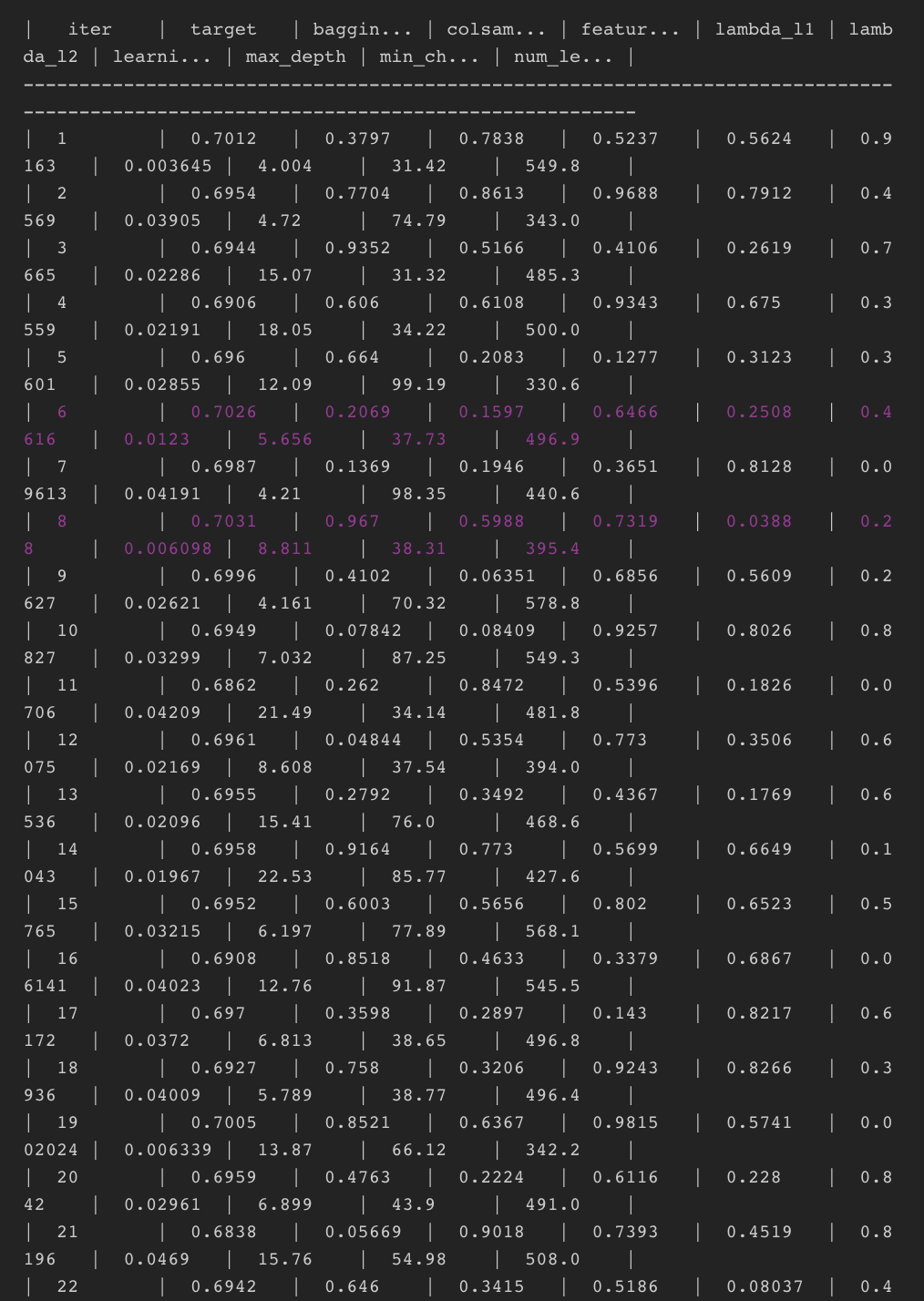

 

 

모델은 최적해를 다음과 같은 방식으로 찾게 되는데 여기서 init_points는 최초 initialize되는 랜덤 5회를 돌리고 그다음 n_iter만큼 추가 반복하여 최적해를 찾는데 만약 데이터가 작고 모델이 가볍다면 init_points와 n_iter를 더 높여서 찾으면 더 성능이 좋은 파라미터를 찾을 수 있게됩니다.

 

마지막으로 도출된 해는 다음과 같이 찾을 수 있습니다.

 

 

6. 마치며

베이지안 최적화에 대해서 알아봤는데요. 위에서 너무 베이지안이 최고야! 라는 식으로 글을 적은 것 같은데 무조건은 아니지만 실제로 ML에서는 시간적 비용, 성능 측면을 같이 고려했을 때 BO방식이 가장 좋은 방식인 것을 알 수 있었습니다. BO에도 들어가는 파라미터 acquisition, surrogant 등의 많은 파라미터가 있는데 이부분도 스터디를 진행한 다음 파라미터를 찾는다면 더 효과적인 파라미터 탐색으로 이어질 수 있을 것 같습니다.

 

다음 포스팅은 위에서 같이 리스트한 Random, Grid 등의 다른 파라미터 최적화 방법론에 대해서 알아보고 실제로 어떤 방식으로 접근했을 때 효과적인 방법론인지 시간, 성능 두가지 KPI로 설명드리겠습니다. 감사합니다.